Swin Transformer
简述
可以作为CV任务中通用的backbone,根据作者给出的实验结果,应用在图像分类、目标检测、语义分割等方面都有比较好的效果。
将transformer提取的特征,转化成了与CNN相似的形式。先前的transformer结构,都是将图像按照类似NLP任务中的方法,将图像直接输入到transformer中。例如ViT,就是将图像拉成一个1-D向量处理,而且在所有layer中,都会保持固定的分辨率,这样对于图像任务,特别是对于语义分割这样的,需要进行密集预测的任务,运算量会非常大,自注意力运算的复杂度是图像大小的平方复杂度。swin-transformer采用的是金字塔层次结构,利用Patch merging降低特征图分辨率。这样做的好处是能够便于进行多尺度预测,处理物体规模大小变化较大的情况。对于自注意力的计算,Swin-transformer使用的是窗口计算自注意力,能够实现对于图像像素线性的计算复杂度。而且能够实现与CNN相同的特征图尺寸,能直接替换使用在一些例如Unet这样的网络架构中。
根据作者的说法,Swin-transformer的关键设计是使用了ShiftedWindows。因为窗口计算注意力,窗口之间的patch并没有连接,所以使用shifted来增强建模能力。主要贡献是提出了一种视觉任务的通用transformer backbone,且速度较快。
网络结构
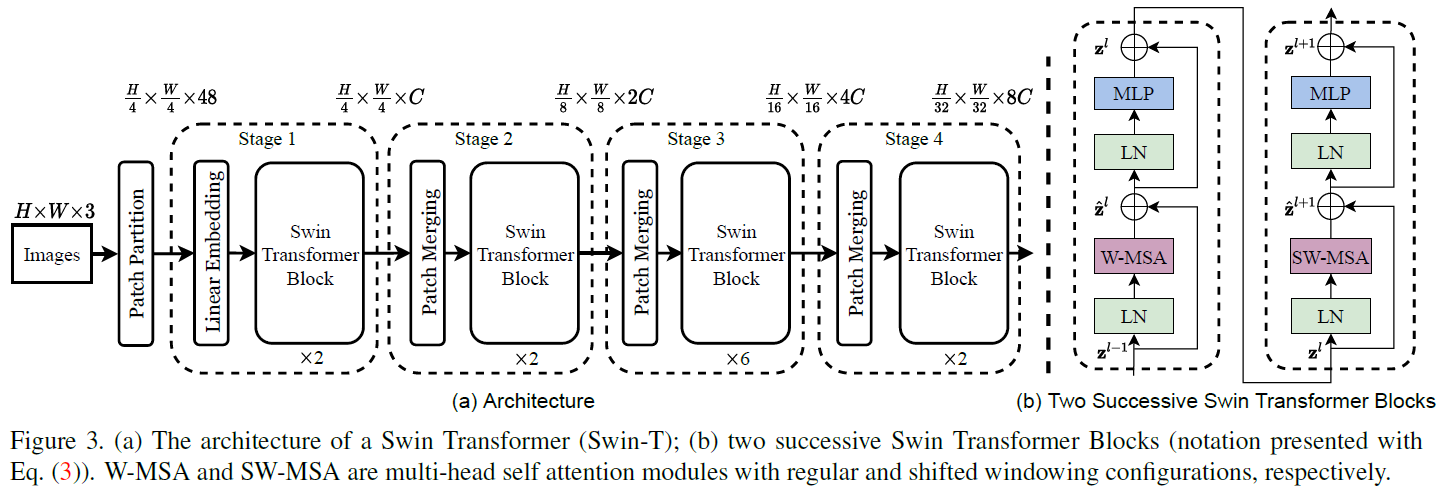
对于一个三通道RGB输入,首先划分4*4大小范围内作为一个patch,这个划分要远小于ViT中16*16的patch划分.这样做是希望能够捕获小尺度的图像特征,类似于CNN的做法.
完成对图像Patch的划分后,此时图像的特征为$48*HW/16$(3通道图像4*4大小),接下来是对Patch进行Embedding,嵌入后,将一个48维的特征嵌入到C维空间中,送入两个连续的Swin-Transformer Block中处理.每个Stage中均包含两个Block,这两个Block先执行W-MSA,紧接着后一个执行SW-MSA,如图右侧所示.
W表示的是Window,小尺寸的patch划分对小尺度特征较为友好,但是这样一来,在Attention层中的计算量会变得非常大(计算复杂度$\propto(hw)^2$,w和h为图像横纵切分的patch数量).作者提出了使用Window注意力来解决这个问题,将原来的全局MSA变为计算在Window内的patch之间的注意力.计算复杂度如下(来源于原paper,M为Window内每条边切分的patch数量): \(\Omega(MSA) = 4hwC^2 + 2(hw)^2C\\ \Omega(W-MSA) = 4hwC^2 + 2M^2hwC\) 但是这样又会出现一些其他问题,本身窗口化可以认为是相邻的位置图像特征可能相关联,这样可以看做是局部注意力.这样划分后,相邻窗口的边缘本身位置相邻的特征就会被割裂开,影响真实特征提取的效果,因而使用一个SW-MSA来修正这一问题,保证跨窗口的特征也能被很好的提取.

具体计算中,使用了Shifted方法来加快边缘不完整window的计算,在计算结束后求attention时使用mask掩膜来屏蔽掉shifted区域即可.在Attention时按照正常计算,在softmax这一步中,减去一个非常大的负值,就可以完成对非本窗口区域的屏蔽.
Patch融合是将$2\times 2$邻域内的$2\times 2 \times C$像素变成$1\times 1 \times 4C$,缩小特征图尺寸,并增加通道数.然后通过一个线性层,映射到$1\times 1 \times 2C$实现了特征降维,类似于在第一对blocks的基础上,进一步做了Embedding.
这样就对特征层实现了尺寸缩小通道增加,类似于CNN中卷积的过程,特征图尺寸缩小,同时特征通道数增加.
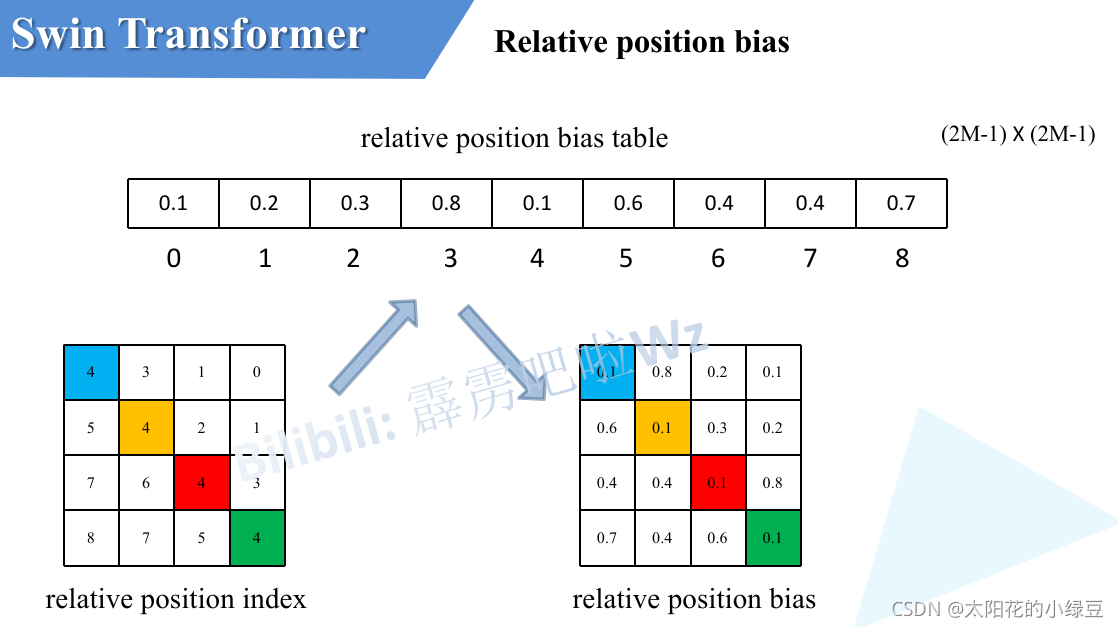
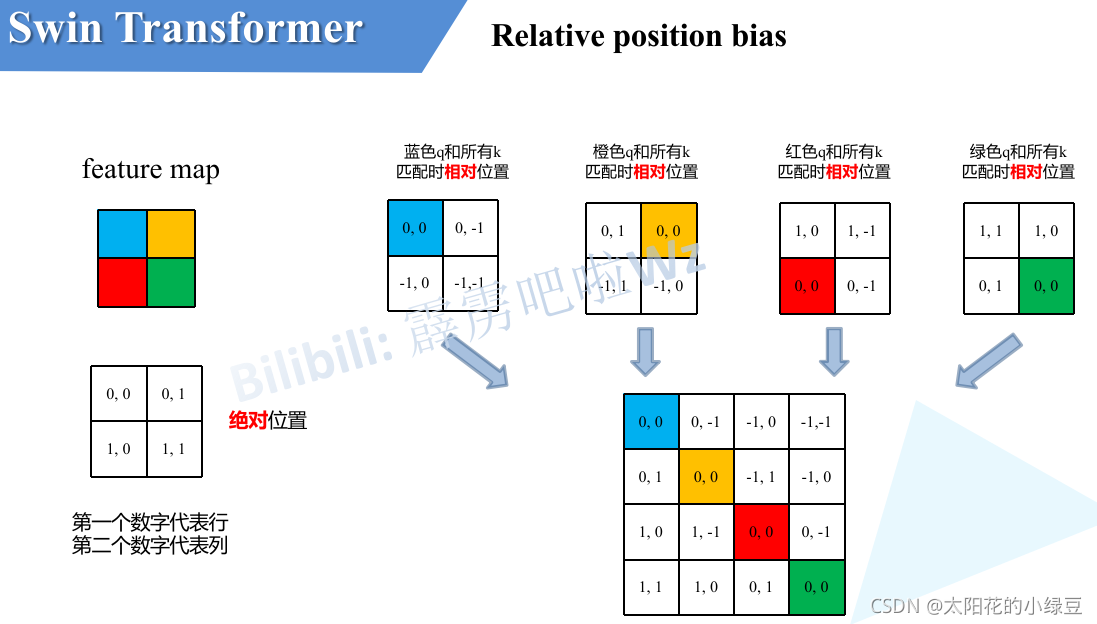
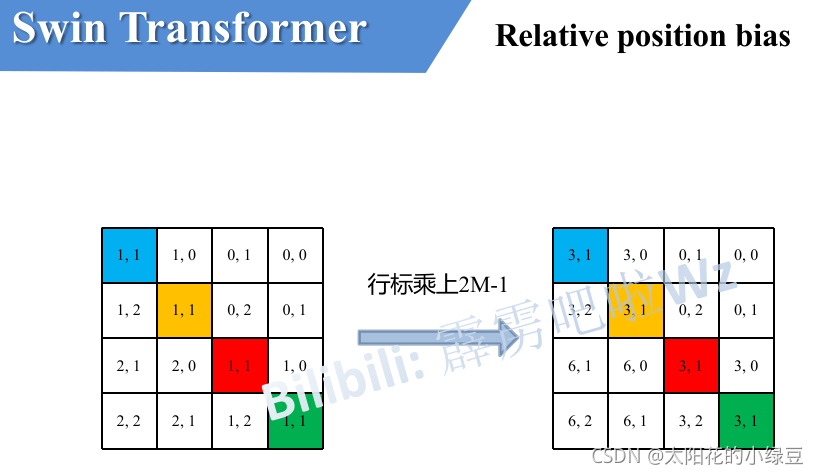
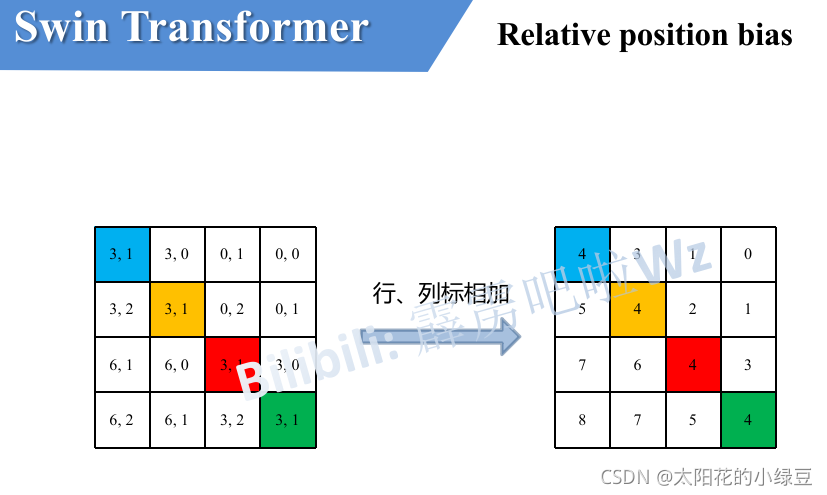
相对位置编码在一个Window中计算注意力时使用,一个窗口含有$M\times M$个token,但是实际上由于相对位置仅限$[-M+1,M-1]$(离散取值),所以只需要构建$(2M-1)\times(2M-1)$个相对位置的值,而不是需要$M^2\times M^2$个相对位置编码.

https://www.bilibili.com/video/BV1pL4y1v7jC?share_source=copy_web
\[Attention(Q,K,V) = Softmax(\frac{QK^T}{\sqrt{d_k}}+B)V\]$Q, K, V\in \mathbb{R}^{M^2\times d}, B\in \mathbb{R}^{M^2\times M^2}$,上文所述的相对位置编码计算规则则是将$B$简化为$\hat B \in \mathbb{R}^{(2M-1)^2}$,需要$B$时,从$\hat B$中查询得到对应的值即可.
图像分割Swin-UNet
#TODO